What’s So Special about a Square?

In my last discussion about squares, and what students think about them, I showed many examples of squares that students had drawn. Approximately 80 percent of them were drawn correctly. Those that weren’t drawn correctly were rectangles–every one. The rectangle drawers, though they did not attend to the single aspect that would ensure their drawing was a square, drew their shapes with a few ideas in mind. Every drawer adhered to these rules: each drawing had four sides, opposite sides were parallel, and every angle in the figure was 90 degrees. The last item should be considered further.

I have never had a student that did not realize the angles inside rectangles must be 90 degrees, or right. In fact, when I tell them that they drew a rectangle, but not a square, their first defense is that the angles are drawn correctly. The next is a discussion comparing squares and rectangles that concludes with the idea that all squares are rectangles but not all rectangles are squares.

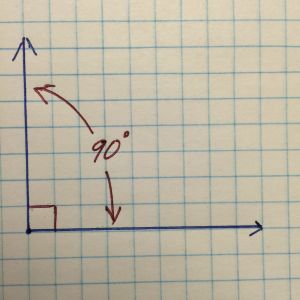
As soon as kids are formally introduced to angle measurements, they are bombarded with questions about 90 degree angles. There are many things discussed during these lessons–the 360 measurement of a complete rotation, 180 degrees in half, 90 in a quarter turn–is this why 90 degree corners are so important? We learn the use of a protractor for creation and measure of any angle and place special emphasis on the angle that represents half of the protractor.  The conversation then progresses toward a new name for a 90 degree intersection–perpendicular. From this moment on, every time there are angles present in a lesson questions about whether intersections are perpendicular dominate problem sets.

Something of great importance, rarely spoken of, has occurred right under our very noses. A progression of ideas starting with a ray,

sharing an end-point with another ray,

and then separated to a degree so significant that it not only needs its own name,

but we can’t seem to stop asking kids about it. But why?

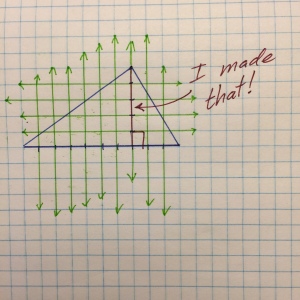
The answer is actually very simple. Imagine trying to find the area of a figure without ensuring a perpendicular relationship between two of the edges.

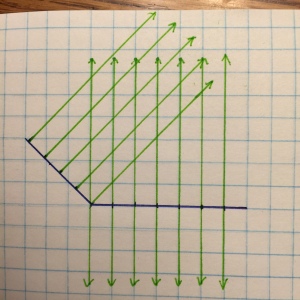
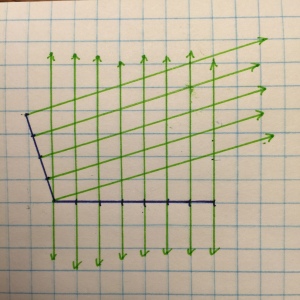
What are those on the left? Parallelograms, triangles, and trapezoids? How in the world are you supposed to define the area of a polygon if the units you’ve created inside are not uniform? They are a little better in the middle, but on the right . . . oh, yeah. That’s more like it. The units that are created inside the polygon are exactly alike and can now be referenced as “square units.”

When the edges of the figures won’t work for us, we can make our own!

Even from outside!

The incredible thing here is that if you want to define the area of a polygon, you must do one of two things–establish a perpendicular relationship between two of the edges or force a perpendicular relationship between one of the existing edges and one of your creation. If you don’t, area cannot be defined. Period. That is why it is so incredibly important that we are able to recognize when perpendicular relationships exist and when they don’t.

Ah, but if we are using edges and 90 degree angles and you say we can’t find the area of anything until we compare edges, how do we find the area of a circle?

 

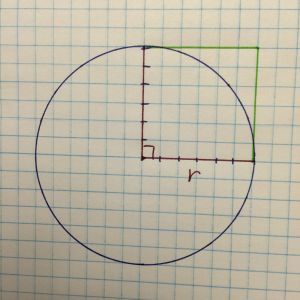
Good question. What if I used something that I knew about the circle but wasn’t necessarily part of it? Maybe something like its radius?

And since the radius isn’t really perpendicular to the curve of the circle, let’s find something else to create a 90 degree angle. How about itself? In other words–square the radius.

Sure looks like a square to me. If we extend it around the area of the circle…

and only pay attention to the inside, we have what we were looking for.  The area of the circle is approximately 3.14 of our squared radius. That’s right–Area equals Pi times the radius squared, but that is a topic for another time.